開篇宣告:1:以下內容轉自以下內容轉自微信公眾號醫咖會《被誤解的P值》,如有侵權,可聯絡刪除
2. 以下觀點,僅代表作者個人觀點,請帶著質疑的態度去閱讀。如有問題,歡迎評論區留言或直接聯絡作者
P值一直是臨床研究中評估結果統計學顯著性的核心指標,雖應用廣泛,卻常遭誤讀,從而可能對臨床決策產生負面影響。本文整理自《Br J Anaesth》發表的一項社論[1],探討了P值的常見認知誤區、過度依賴P值的後果、以及最佳化結果解讀的方法。
P值的常見誤解
P值最常見的誤解之一,是認為P值代表原假設為真的機率。許多人錯誤地認為,P值為0.05意味著該結果有5%的機率是偶然產生的。正如Staffa和Zurakowski[2,3]強調的那樣,P值常常在缺乏效應值或置信區間的情況下被報告,導致混淆或錯誤解讀。這種誤解往往使人們對具有統計學顯著性的結果過度自信。
另一個常見誤區,是認為僅憑P值就能決定研究結果的有效性或重要性。通常,如果P值<0.05,結果被認為“顯著”,但這一做法忽略了一個重要事實:統計學顯著性並不等同於臨床重要性。即使某項研究的樣本量很大,並得出了具有統計學顯著性的P值,其效應值(effect size)可能極小,以至於在實踐中並無實際意義[4]。
多重比較中的I類錯誤
顯著性檢驗存在一定程度的誤差,包括I類錯誤和II類錯誤。I類錯誤(假陽性)指錯誤地拒絕原假設,即實際上不存在效應卻被判定為存在;II類錯誤(假陰性)則是錯誤地接受原假設,即實際存在效應卻被判定為不存在。
在臨床試驗中,當單個研究進行多重比較時就會出現多重性問題[5]。隨著統計檢驗次數的增加,I類錯誤的發生率會放大。族錯誤率(即一組假設檢驗中至少出現一次I類錯誤的機率)會隨著檢驗次數的增加而上升。
多重性可能出現在多種場景中,包括:多個亞組間的比較、多個治療組的評估、多個結局指標的測定,或對同一結局指標在不同時間點的分析[6]。
研究者通常採用事後分析方法(如Bonferroni校正)來修正這一問題,透過將預設的α水平(通常為0.05)除以比較次數來調整顯著性閾值。例如,進行10次比較的研究,其校正後的閾值將變為0.005,這有助於降低I類錯誤的發生機率[7]。然而,將P值閾值降至0.005也可能帶來重大挑戰。
過度依賴P值的後果
臨床研究中對P值的過度依賴引發諸多不良趨勢。首要問題是發表偏倚,即P值更小的研究更容易獲得發表機會,這種偏倚可能扭曲證據基礎,最終導致採用無效甚至有害的治療方案[8]。
更值得警惕的是,為追求P值<0.05,部分研究者可能採取"P值操縱(P-hacking)"等不端行為,即透過多種方式反覆分析資料直至達到顯著性標準[9]。
Greenland[10]指出,儘管P值本身設計合理,但濫用和誤解現象普遍存在,常導致研究結論被錯誤批判或不當應用。為此他建議採用S值來替代,該指標透過位元(bits)量化關聯強度,能有效降低資料誤讀風險。S值是P值的負二進制對數變換,用於衡量資料相對於背景假設、模型及檢驗假設的資訊量。
例如,P值0.05對應的S值為4.32位元,其為意外的程度僅略高於連續四次擲硬幣均出現正面的情況。當P值趨近於零時,S值的位元數將遞增,使其成為更直觀的證據強度評估指標[11]。
P值的替代方案
鑑於P值的侷限性,我們需要能更好體現臨床意義的評估指標。最小臨床重要差異(MCID)正是這樣一種指標,代表患者能夠感知的最小療效差異,且該差異足以改變臨床決策[12]。
與僅關注統計顯著性的P值不同,MCID從患者角度強調研究結果的實際價值。例如,評估新型鎮痛技術時,研究者不應僅關注疼痛評分是否具有統計學意義的下降,更需考量這種改善是否達到提升患者生活質量的程度。
在樣本量、統計效能與臨床意義的關係方面,必須認識到傳統效能計算往往只追求統計顯著性而忽視實際價值。基於MCID計算樣本量可確保研究具備檢測臨床相關差異的統計效能。此外,參照MCID解讀效應估計值及其置信區間,能突顯研究結果的實踐意義,幫助臨床醫生判斷結果是否足以改善診療實踐。
來看一個假設案例:
某研究評估新型鎮痛藥對術後疼痛的管理效果,結果顯示疼痛評分顯著降低(P=0.03)。然而在10分量表上,疼痛評分僅降低1分。若不考慮最小臨床重要差異(MCID),這一結果可能被解讀為藥物有效的證據。但若該疼痛量表的MCID確定為2分,則研究觀察到的改善並未達到臨床意義閾值。此時,儘管P值具有統計學顯著性,該治療方案仍不能被認定為臨床有效。這個案例展現了將MCID與統計分析結合的重要性——唯有如此,才能準確理解研究結果的臨床價值。
Benjamin與Berger[13]對改進P值使用提出了重要建議,主張在更科學的框架下運用P值,並與其他統計指標結合使用。他們提出的改革方案包含三大核心要素:
1、建議將顯著性閾值從0.05降低至0.005,以提升證據強度;
2、推薦在報告P值時同步呈現貝葉斯因子邊界值(BFB),避免對結果顯著性的過度解讀;
3、強調採用貝葉斯分析方法整合研究證據——透過將貝葉斯因子與先驗機率結合,實現對研究結果的更全面評估。
除MCID外,建議在統計推斷中常規使用效應值的置信區間(CI)。效應值及其CI應與P值配合報告,這種"三位一體"的呈現方式能更完整地詮釋研究結果:CI不僅反映估計精度,還展示真實效應值可能存在的範圍,使研究者能清晰把握效應值的不確定性。
圖1系統總結了研究者可採用的輔助方法,這些方法與P值互為補充,能顯著提升結果解讀的科學性與臨床價值。
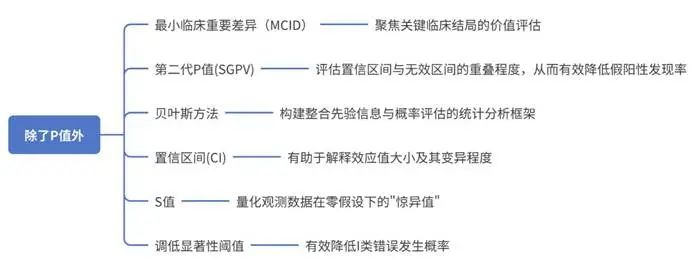
圖1. 除P值外可增強研究結果有效性的方法總結
參考文獻
1. Br J Anaesth. 2025;134(4):909-913.
2. J Thorac Cardiovasc Surg 2022; 164: e37e8
3. J Thorac Cardiovasc Surg 2021;161: 1367e72
4. Am Stat 2016; 70: 129e33
5. Int J Epidemiol 2017; 46: 746e55
6. JAMA Netw Open 2020; 3, E203082
7. Int J Epidemiol 2017; 46: 746e55
8. BMJ 2001; 322: 226e31
9. AANA J 2016; 84: 305e8
10. Am Stat 2019; 73: 106e14
11. Glob Epidemiol 2022; 4, 100085
12. Control Clin Trial. 1989; 10: 407e15
13. Am Stat 2019; 73: 186e91
完結












0則評論