开篇声明:1:以下内容转自以下内容转自微信公众号医咖会《被误解的P值》,如有侵权,可联系删除
2. 以下观点,仅代表作者个人观点,请带着质疑的态度去阅读。如有问题,欢迎评论区留言或直接联系作者
P值一直是临床研究中评估结果统计学显著性的核心指标,虽应用广泛,却常遭误读,从而可能对临床决策产生负面影响。本文整理自《Br J Anaesth》发表的一项社论[1],探讨了P值的常见认知误区、过度依赖P值的后果、以及优化结果解读的方法。
P值的常见误解
P值最常见的误解之一,是认为P值代表原假设为真的概率。许多人错误地认为,P值为0.05意味着该结果有5%的概率是偶然产生的。正如Staffa和Zurakowski[2,3]强调的那样,P值常常在缺乏效应值或置信区间的情况下被报告,导致混淆或错误解读。这种误解往往使人们对具有统计学显著性的结果过度自信。
另一个常见误区,是认为仅凭P值就能决定研究结果的有效性或重要性。通常,如果P值<0.05,结果被认为“显著”,但这一做法忽略了一个重要事实:统计学显著性并不等同于临床重要性。即使某项研究的样本量很大,并得出了具有统计学显著性的P值,其效应值(effect size)可能极小,以至于在实践中并无实际意义[4]。
多重比较中的I类错误
显著性检验存在一定程度的误差,包括I类错误和II类错误。I类错误(假阳性)指错误地拒绝原假设,即实际上不存在效应却被判定为存在;II类错误(假阴性)则是错误地接受原假设,即实际存在效应却被判定为不存在。
在临床试验中,当单个研究进行多重比较时就会出现多重性问题[5]。随着统计检验次数的增加,I类错误的发生率会放大。族错误率(即一组假设检验中至少出现一次I类错误的概率)会随着检验次数的增加而上升。
多重性可能出现在多种场景中,包括:多个亚组间的比较、多个治疗组的评估、多个结局指标的测定,或对同一结局指标在不同时间点的分析[6]。
研究者通常采用事后分析方法(如Bonferroni校正)来修正这一问题,通过将预设的α水平(通常为0.05)除以比较次数来调整显著性阈值。例如,进行10次比较的研究,其校正后的阈值将变为0.005,这有助于降低I类错误的发生概率[7]。然而,将P值阈值降至0.005也可能带来重大挑战。
过度依赖P值的后果
临床研究中对P值的过度依赖引发诸多不良趋势。首要问题是发表偏倚,即P值更小的研究更容易获得发表机会,这种偏倚可能扭曲证据基础,最终导致采用无效甚至有害的治疗方案[8]。
更值得警惕的是,为追求P值<0.05,部分研究者可能采取"P值操纵(P-hacking)"等不端行为,即通过多种方式反复分析数据直至达到显著性标准[9]。
Greenland[10]指出,尽管P值本身设计合理,但滥用和误解现象普遍存在,常导致研究结论被错误批判或不当应用。为此他建议采用S值来替代,该指标通过比特(bits)量化关联强度,能有效降低数据误读风险。S值是P值的负二进制对数变换,用于衡量数据相对于背景假设、模型及检验假设的信息量。
例如,P值0.05对应的S值为4.32比特,其为意外的程度仅略高于连续四次掷硬币均出现正面的情况。当P值趋近于零时,S值的比特数将递增,使其成为更直观的证据强度评估指标[11]。
P值的替代方案
鉴于P值的局限性,我们需要能更好体现临床意义的评估指标。最小临床重要差异(MCID)正是这样一种指标,代表患者能够感知的最小疗效差异,且该差异足以改变临床决策[12]。
与仅关注统计显著性的P值不同,MCID从患者角度强调研究结果的实际价值。例如,评估新型镇痛技术时,研究者不应仅关注疼痛评分是否具有统计学意义的下降,更需考量这种改善是否达到提升患者生活质量的程度。
在样本量、统计效能与临床意义的关系方面,必须认识到传统效能计算往往只追求统计显著性而忽视实际价值。基于MCID计算样本量可确保研究具备检测临床相关差异的统计效能。此外,参照MCID解读效应估计值及其置信区间,能突显研究结果的实践意义,帮助临床医生判断结果是否足以改善诊疗实践。
来看一个假设案例:
某研究评估新型镇痛药对术后疼痛的管理效果,结果显示疼痛评分显著降低(P=0.03)。然而在10分量表上,疼痛评分仅降低1分。若不考虑最小临床重要差异(MCID),这一结果可能被解读为药物有效的证据。但若该疼痛量表的MCID确定为2分,则研究观察到的改善并未达到临床意义阈值。此时,尽管P值具有统计学显著性,该治疗方案仍不能被认定为临床有效。这个案例展现了将MCID与统计分析结合的重要性——唯有如此,才能准确理解研究结果的临床价值。
Benjamin与Berger[13]对改进P值使用提出了重要建议,主张在更科学的框架下运用P值,并与其他统计指标结合使用。他们提出的改革方案包含三大核心要素:
1、建议将显著性阈值从0.05降低至0.005,以提升证据强度;
2、推荐在报告P值时同步呈现贝叶斯因子边界值(BFB),避免对结果显著性的过度解读;
3、强调采用贝叶斯分析方法整合研究证据——通过将贝叶斯因子与先验概率结合,实现对研究结果的更全面评估。
除MCID外,建议在统计推断中常规使用效应值的置信区间(CI)。效应值及其CI应与P值配合报告,这种"三位一体"的呈现方式能更完整地诠释研究结果:CI不仅反映估计精度,还展示真实效应值可能存在的范围,使研究者能清晰把握效应值的不确定性。
图1系统总结了研究者可采用的辅助方法,这些方法与P值互为补充,能显著提升结果解读的科学性与临床价值。
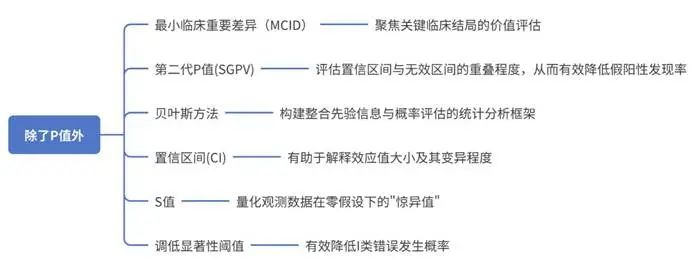
图1. 除P值外可增强研究结果有效性的方法总结
参考文献
1. Br J Anaesth. 2025;134(4):909-913.
2. J Thorac Cardiovasc Surg 2022; 164: e37e8
3. J Thorac Cardiovasc Surg 2021;161: 1367e72
4. Am Stat 2016; 70: 129e33
5. Int J Epidemiol 2017; 46: 746e55
6. JAMA Netw Open 2020; 3, E203082
7. Int J Epidemiol 2017; 46: 746e55
8. BMJ 2001; 322: 226e31
9. AANA J 2016; 84: 305e8
10. Am Stat 2019; 73: 106e14
11. Glob Epidemiol 2022; 4, 100085
12. Control Clin Trial. 1989; 10: 407e15
13. Am Stat 2019; 73: 186e91
完结
















0条评论