开篇声明:1:以下内容转自以下内容转自微信公众号流行病与卫生统计学《PFS区间删失的样本量估计》,如有侵权,可联系删除
2. 以下观点,仅代表作者个人观点,请带着质疑的态度去阅读。如有问题,欢迎评论区留言或直接联系作者
ABSTRACT
无进展生存期(PFS)经常用作肿瘤后期疾病的II和III期研究中的主要终点。 PFS是从入组到疾病进展或死亡的持续时间,以先发生为准。直到下一次预定评估(区间删失)或在进展前发生死亡时,才能观察到疾病进展的实际发生。对数秩检验通常用于比较对PFS的治疗效果。 PFS的样本量无需调整区间删失或考虑到生存的危害比率很可能会使所需功率降低。不幸的是,用于样本量计算的主要软件(例如NQueryAdvisor®,SAS®,Pass和East®)没有此功能。本文中展示的SAS宏集中在这种未满足的需求。
Key words: survival analysis, progression-free survival, staggered enrollment, power s imulation, timeline projection.
INTRODUCTION
无进展生存期 (PFS) 经常被用作肿瘤晚期疾病II期和III期研究的主要终点。PFS是从入组到疾病进展或死亡的持续时间,以先发生者为准。在下一次预定评估 (区间删失) 之前或死亡发生之前,无法观察到疾病进展的实际发生 (区间删失) 。例如,如果患者A和B的疾病进展的实际 (未知) 时间分别发生在4.2和5.6个月,并且假设评估每隔一个月进行一次,则观察到的PFS为6个月。
对数秩检验通常用于比较对PFS的治疗效果。基于对数秩检验的PFS的样本量,而无需调整区间删失或考虑到生存的危害比率很可能会使所需的功率降低。不幸的是,样本量计算的主要软件(例如,NQuery Advisor,SAS,Pass和East)没有此功能。由于事件的数量确定了logrank检验的功能,在监管环境中,该分析的数据截止日期应由要包括在分析中的事件数量。考虑到要入组的患者数量以及要观察的事件数量,本文中证明的SAS宏介绍了区间删失以及TTP和PFS功率模拟中TTP和生存的分布。该宏还估计何时发生预先指定的事件数量。除了PFS(是连续和区间删失数据的混合物)外,我们还展示了将此宏的应用扩展到连续终点和区间删失终点。
THE ALGORITHM OF THE MACRO
附录中的宏中插入了一些注释。由于空间限制,本节仅说明了宏中重要且更复杂的代码。宏包括以下 4 个主要步骤:
1. 生成模拟中指定的所有试验的数据,包括入组时间、生存期、实际和观察到的 TTP 和 PFS。
2. 确定每个试验中预定数量的事件何时发生,并确定观察是否被删失。
3. 使用 SAS LIFETEST 程序和 ODS 计算并输出每个试验的 PFS 中位数和 logrank p 值。
4. 根据前一步获得的结果估计功率并预测时间表。
SIMULATION OF STAGGERED ENROLLMENT
临床试验的入组率通常会在试验地点开始时经历一个类似斜坡的时期(图1中的区间[0,tA])。然后入组率稳定下来(图1中的区间(tA,tB))。

SIMULATION OF THE OBSERVED PFS
指数分布用于模拟TTP和生存的实际事件时间。模拟的实际PFS是这两个值的最小值。设x为对照组的中位事件发生时间,对照组与试验组的危险比为h,其中h>1。则对照组的平均值为x / log(2),其中log(·)是自然对数函数。对于指数分布,中位事件发生时间的百分比改善等于100×(h - 1)%。因此,试验组的中位数和平均数分别为hx和hx / log(2) 。
SAS 函数 ranexp(⋅) 使用括号中的随机化种子,生成参数为 1 的指数随机变量。可以直接证明,对于任何非负 y,y[ranexp(⋅)] 生成平均为 y 的指数随机变量。此属性用于生成 TTP 和生存。
所观察到的PFS的模拟是从模拟生存和模拟观察到的TTP中的最小值得出的。生存和实际TTP的模拟遵循前面讨论的方法。观察到的TTP可以通过以下方式模拟:
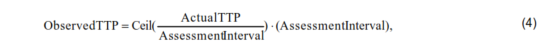
其中 Ceil(⋅) 是大于或等于参数的最小整数。例如,如果实际疾病进展发生在入组后 4.5 个月,并且每 2 个月进行一次评估,则观察到的 TTP 为 Ceil(4.5/2)x2 = 3x2 = 6(个月)。PFS 的日历时间为 PFS 加上入组时间。
POWER SIMULATION
数据按每项试验的 PFS 日历时间排序,并确定观察预定事件数量的日历时间。在此时间点之后入组的患者在每项试验中被淘汰。对于其余患者,在此截止时间之后观察到的 PFS 在截止时间被剔除。所得数据用于使用 LIFETEST 程序计算每项试验的双侧对数秩 p 值和观察到的 PFS 中位数。估计的功率是 p 值小于或等于显著水平的试验数量的比例。

EXAMPLES
EXAMPLE 1
宏还使用Schoenfeld(1982)公式生成了连续数据所需事件的数量。
使用Sschoenfeld公式中的事件数量,此示例验证了宏对连续数据模拟的功率是否会产生预期功率。此示例还显示了如何将宏应用到连续数据。该宏以TTP的提高50%(危险比= 1.5),一对一的随机分配,功率90%,双侧显着性水平为0.05。使用Schoenfeld的公式为256所需事件的数量。为了验证这一数量的事件是否可以通过宏观实现90%的功率,我们还使用256名0脱落率的患者。换句话说,所有患者都将遵循直到进展。
評估區間分配一個小數值 (0.0001) ,以便觀察到的 TTP 成為連續的。对照組和试验組的中位總生存期分配兩個大數值,使得模擬的 PFS 與連續 TTP 相同。使用 2000 次試驗,估計功率和 95% 置信區間分別為 0.897 和 (0.875、0.919) 。
在中位 TTP 等於 10 的情況下,達到 256 個事件的平均時間相當長 (128.42) ,置信區間很寬 (97.58,186.19) 。這是因為指數分佈的長尾。由於空間限制,SAS 輸出不會顯示。
EXAMPLE 2
假设一项临床试验旨在检测 PFS 的差异,其中 TTP 的中位为 14 个月对 20 个月,中位生存期为 56 个月对 62 个月。每 12 周 (2.76 个月) 评估一次疾病进展。如果使用 TTP 计算样本量而不考虑生存率,则在不调整区间删失的情况下达到 80% 功效所需的事件数为 247。在调整了区间删失并考虑了生存后,所需的事件数约为 390 个,比 247 个增加了 58%!
宏的输出如下所示

CONCLUSION
本文演示的 SAS 宏在设计时同时考虑了临床和统计。通过每月的爬坡期、总入组期和每月入组率,临床运营人员可以规划启动多少个研究中心以及何时完成研究中心启动。或者,临床作人员可以提供启动最大入组率和所有研究中心启动时间。然后,项目统计师可以使用此宏计算总入组期和项目进行最终分析的时间。由于假设入组率从 0 线性增加,因此应调整非线性入组以达到达到精确的预测。爬坡期的开始应该是第一位患者入组的月份,爬坡期的终点应该是入组率稳定的月份。例如,如果一项临床试验的第一个中心在 1 月启动,第一个患者在 2 月入组,所有中心都在 6 月启动,并且该试验直到同年 9 月才为公众所熟知,那么爬坡期的起点和终点应该是 2 月和 9 月。
使用较少的模拟试验,例如500,直到估计功率接近所需的功率,可以通过尝试和错误近似ttp或pfs的所需事件。考虑到任何中值和危险比,您可以首先通过一个试验运行宏,以获取连续数据所需的事件数量。然后将此数字分别为所需的事件数量和样本量加倍和三倍。微调样本量和事件数量,直到估计功率接近预期功率。达到所需精度所需的功率模拟的试验次数可以从等式(6)得出。
FDA 指出,一些三期临床试验功效不足。 例 2 的结果与 FDA 的声明相呼应。在规划使用 PFS 作为主要终点的临床研究时,考虑区间删失和生存率非常重要。这是由于以下原因:
1。直到下一次预定评估才能观察到实际进展的实际事件时间。因此,具有不同实际TTP的患者可能具有相同的观察到的TTP。
2。尽管中位生存期通常比TTP长得多,但大量PFS事件可能是由死亡引起的。假设分别对实际TTP的指数分布和中位λ1和λ2生存,这很容易表明在进展前发生的死亡的可能性是
λ1/(λ1λ2)。在示例2中,对照组和试验组分别为20%和24%。
3。如果药物有效,则在临床研究中已经表明,生存的改善接近扩展的TTP或PFS。参见Rai等(2000)和Petrylak(2004)。换句话说,危险比的生存改善将比TTP小得多。
本文中介绍的宏解决了上述三个问题。尽管指数分布用于对 TTP 和生存率进行建模,但此宏可以很容易地扩展到 Weibull 或其他生存分布。








REFERENCES
Cytel Inc. (2005), East Version 4 User Manual, Cambridge, MA.
Elashoff, D. (2005), nQuery Advisor Release 6.0 Users Guide, Los Angeles, CA. Hintze, J.L. (2005), PASS User’s Guide – III, NCSS, Kaysville, Utah.
Petrylak, D. (2004), “Docetaxel in HRPC: Data From Recent Randomized Trials,” a presentation made at the Fourth International Prostate Cancer Congress.
Rai, K. R., Peterson, B. L., Appelbaum, F. R., Kolitz J., Elias, L., Shepherd, L., Hines, J., Threatte, G. A., Larson, R. A., Cheson, B. D., Schiffer, C. A. (2000), “Fludarabine Compared With Chlorambucil As Primary Therapy For Chronic Lymphocytic Leukemia,” The New England Journal of Medicine, 343: 1750–1757.
SAS Institute Inc. (1999), SAS/STAT User’s Guide, Version 8. Cary, NC: SAS Institute Inc.
Schoenfeld D.A. (1981), “The asymptotic properties of comparative tests for comparing survival distributions ,”
Biometrika, 68, 316-319.
完结
















0条评论